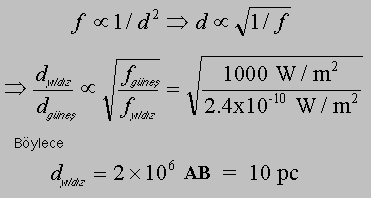DERS 14: YILDIZ
TAYFLARI ve UZAKLIKLARI




Dersin Konuları
-
Yıldızların Tayfları
-
Yıldızların sınıflandırılması
-
Yıldızlara olan uzaklık
-
Yıldızlar ne kadar uzaklıktadır
-
Yıldızların Paralaksları
Tayfsal Sınıflama = Sıcaklık Sıralaması
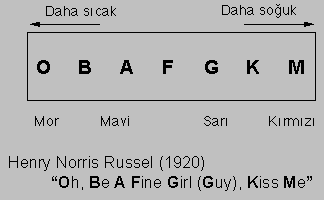
Soğurma Çizgi Bilgisi
|
Sıcaklık
|
Soğurma Çizgileri
|
|
Yüksek
|
İyonize olmuş atomlar
|
|
Orta
|
Nötr (Yüksüz) atomlar
|
|
Düşük
|
Moleküller
|
Tayf Türüne Göre Çizgilerin Şiddeti
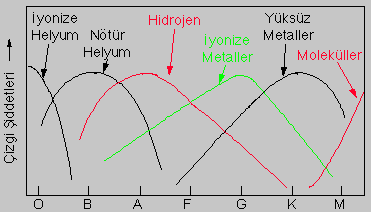
Yıldızların Tayfsal Sınıflaması
|
Tür
|
Sıcaklık (K)
|
Özellikler
|
Örnek
|
|
O
|
28000-60000
|
He II, Si IV, O III
|
Orionis
|
|
B
|
10000-28000
|
He I, Si II, H I
|
Rigel, Spica
|
|
A
|
7500-10000
|
H I, Fe II, Mg II
|
Sirius, Vega
|
|
F
|
6000-7500
|
Nötr metaller, Fe I,
zayıf H I ve Ca II
|
Canopus,
Polarius
|
|
G
|
5000-6000
|
Ca II, Nötr metaller
|
Güneş, Capella
|
|
K
|
3500-5000
|
Nötr metaller,
Moleküler Bandlar, TiO
|
Arcturus, Aldebaran
|
|
M
|
<3500
|
Moleküler Bandlar, TiO,
VO, Nötr Metaller
|
Betelgeuse,
Antares
|
Bu Resim Henüz Tamamlanmış Değildir
-
Bir yıldızın tayf türü (veya sınıfı) bize o yıldızın sıcaklığı konusunda
bilgi vermektedir fakat onun ışınımgücü hakkında bilgi vermemektedir.
-
Işınımgücü bilgisini elde edebilmek için onun uzaklığının bilinmesi gerekmektedir!
-
Ters Kare Yasasını hatırlayınız!
Yıldızların Uzaklıkları
-
Yakın yıldızların uzaklıklarını nasıl ölçüyoruz?
-
Astronomlar paralaktik yöntemi kullanırlar.
-
Bu yöntem surveyor'ların yöntemine çok benzerdir.
Tarama (Surveyor) Yöntemi
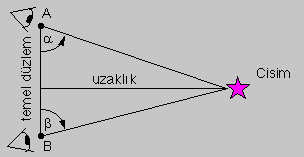
Bir cismi A ve B konumlarından gözlemlediğinizde alfa ve beta açılarını
hesaplayarak ve A ile B arasındaki mesafeyi de ölçerek o cismin uzaklığını
hesaplayabiliriz.
Yıldız Paralaksı
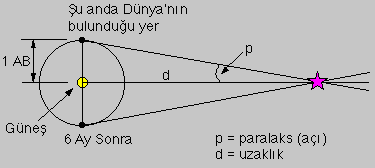
Yakın bir yıldız gökyüzünde uzak yıldızlara (Arkafon Yıldızları) nazaran
konumunu değiştirir.
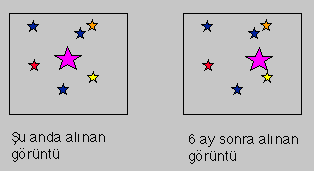
Uzaklıkaları Nasıl Hesaplıyoruz?
Gökyüzünde çok küçük açılı bir üçgen elde ederiz.
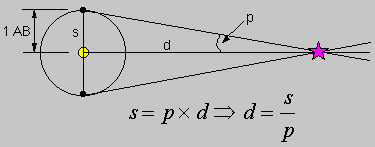
Uzaklığın Hesaplanması
-
Paralaks yay saniyesi olarak ölçülür.
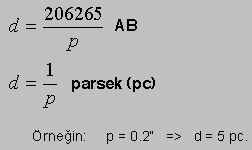
Paralaks Hakkında Not:
-
Daha uzaktaki yıldızlara gidildikçe paralaks değerleride küçülür.
-
Dünyadan ölçülen paralaks değerleri ~0.02" den daha iyi ölçülemez (buda
uzaklık olarak d < 50 pc karşılık gelmektedir).
-
Alpha Cen en büyük paralaksa sahip olan yıldızdır (~0.8")
-
1 pc = 3.26 ly (ışık yılı)
Şu Andaki Durum
-
Hipparcos uydusu 120,000 yıldızın paralaks değerini 0.002" den daha duyarlı
olarak ölçmüştür.
-
=> d < 500 pc
-
Veriler hala işlenmektedir.
Paralaks Yöntemi İle Bulunan Uzaklıkların Önemi
-
Paralaks evrendeki uzaklıkları bilmemiz açısından bir anahtardır.
-
Yakın yıldızlar, evrendeki diğer cisimlerin uzaklıklarını hesaplamak için
basamak taşları olarak kullanılır.
-
Şimdi yıldızların ışınımgüçlerini hesaplayabiliriz!
L, f ve d
-
Işınımgücü, parlaklık (akı) ve uzaklık bilgileri birbirine Ters Kare Yasası
ile bağlıdırlar:
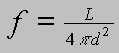
-
Parlaklık ve uzaklık bilinirse L ışınım gücü hesaplanabilir.
Örnek:
-
Güneş'e benzer bir yıldızın gözlenen akısı 2.4x10-10 W/m2
olsun. Eğer bu güneşin Dünya'daki akası 1 kW/m2 ise, bu yıldız
bizden kaç parsek uzaklıktadır?
-
Bu işlemi yapmak için iki yol vardır:
1. Yol: Lgüneş değerini doğrudan hasaplamak
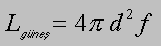
Lgüneş = 4 x 3.14 x (1.5 x 1011 m)2
x 1000 W/m2 = 3 x 1026 W
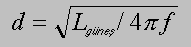
dyıldız = sqrt ( 3 x 1026 W / (4 x 3.14 x 2.4x10-10
W/m2 )) = 3 x 1017 m = 10 pc
2. Yol: Orantı ile
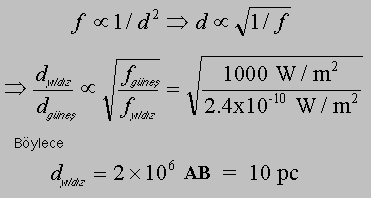
En Yakın Yıldızlar
|
Yıldız
|
Paralaks (")
|
Uzaklık (pc)
|
Işınımgücü (Lgüneş=1)
|
|
Proxima Centauri
|
0.763
|
1.31
|
5 x 10-5
|
|
a Centauri A
|
0.741
|
1.35
|
1.45
|
|
a Centauri B
|
0.741
|
1.35
|
0.40
|
|
Barnard's Star
|
0.522
|
1.81
|
4 x 10-4
|
|
Wolf 359
|
0.426
|
2.35
|
2 x 10-5
|
|
Lalande 21185
|
0.397
|
2.52
|
5 x 10-3
|
|
Sirius A
|
0.377
|
2.65
|
23
|
|
Sirius B
|
0.377
|
2.65
|
2 x 10-3
|
Yıldızların Karşılaştırılması
-
Eğer bütün yıldızalr aynı uzaklıkta olsalardı yıldızların özelliklerini
karşılaştırmak kolay olacaktı.
-
Fakat bunu yapabiliyoruz:
-
Yıldızların uzaklıklarını.
-
Ters Kare Yasasını kullanarak standart bir uzaklıkta iken parlaklığının
ne olacağını bulabiliyoruz.
Mutlak Parlaklık
-
Astronomlar 10pc uzaklığını standart uzaklık olarak kabul etmişlerdir.
-
Bu uzaklıktaki bir yıldızın parlaklığına mutlak parlaklık denir (Mv).
-
Bu yıldızın bünyesel bir özelliğidir!
-
Gökyüzündeki parlaklığı ile ilgili olduğundan bu görünür parlaklıktan farklıdır
(mv).
Görünür (mv) ve Mutlak (Mv) Parlaklık Arasındaki İlişki
-
Bir yıldızın görünür parlaklığının mv = 7.0 olduğunu ve uzaklığının
ise 100 pc uzaklıkta olduğunu kabul edelim.
-
Standart uzaklıktan 10 kez daha uzakda bulunmaktadır.
-
Bu nedenle yıldız standart uzaklıkta bulunsa idi bize 100 kez daha
parlak görünecekti.
-
Yada 5 kadir daha parlak olacaktır. Bu durumda,
-
=> Mv = 2.0
Uzaklık Modülü
Örnekler
-
Deneb yıldızı: mv = 1.26 ve 490 pc uzaklıktadır.
-
mv - Mv = - 5 + 5 log10( d )
1.26 - Mv = - 5 + 5 log10( 490 ) = -8.5
=> Mv = -7.2
-
Güneş: mv = -26.8, d = 1 AU
-
-26.8 - Mv = - 5 + 5 log10( 1/206265 )
=> Mv = 4.8










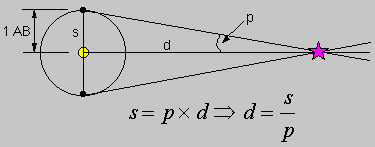

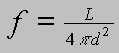
![]()